State Estimation: Python Project.

Guide Professor: Mani Bhushan

I have included the major steps & evaluations for the project in this blog. For a detailed look at the code, check out the notebook file at my Github. here

Introduction

The Williams–Otto reactor is one unit of the Williams–Otto plant model (Williams and Otto, 1960). The estimation relevant problem presented here has been taken from Varshney et al. (2019). The reactor is a CSTR with mass holdup W (kg) and temperature T (K). The reactor is fed with two pure component reactant streams \(F_A\) and \(F_B\) .

Problem Statement

States \(X_B , X_C , X_G, X_P\) are considered to be measured, while states \(X_A , X_E\) are unmeasured and need to be estimated. Further, it is assumed that the standard deviations of unmeasured disturbances affecting the states are 0.5% of the steady state values of the corresponding states. (\(X_i\) - Mole fraction of ith component in reactor.)

Steps

1) Generating State Space Model: \(x(k+1)=F(x(k),u(k)) + w(k)\); where \(F(x(k),u(k))\)represents integration of the original from time \(t(k)\) to \(t(k+1)\) and w(k) is noise.

The non-linear differential equations: -

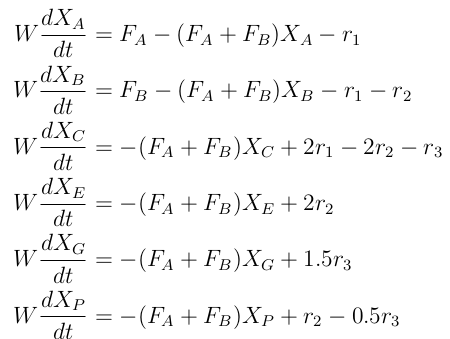
2) Implementing Kalman Filter: Implement Kalman filter (KF), the minimum variance unbiased estimator & Extended KF; Get the estimated states: A & E.

Algorithms for both: -

Plots for States A & E

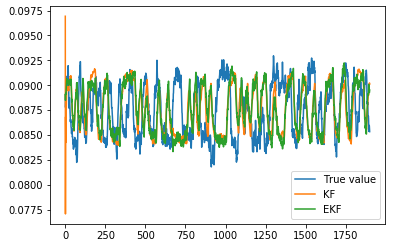
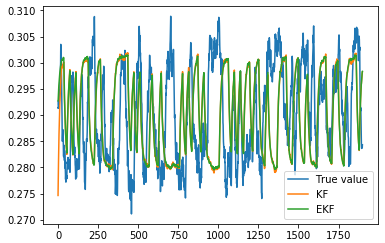
Evaluation Metrics & Code

I have included the major steps & evaluations for the project in this blog. For a detailed look at the code, check out the notebook file at my Github. here